Le obbligazioni sono degli strumenti d’investimento con un livello di rischio che può essere più o o meno alto. Per scegliere quali obbligazioni comprare è necessario tenere in considerazione alcuni concetti chiave come ad esempio il prezzo e il rendimento del titolo obbligazionario e ovviamente tutto quello che riguarda i tassi d’interesse. Anche se spesso si tende a tralasciarli, vanno tenuti in considerazione anche il rischio di tasso e il rischio di duration.
Ma cos’è quest’ultimo? In questa guida approfondiremo proprio questo discorso, rispondendo a quelle che sono domande classiche in relazione a questo argomento. Anzitutto la definizione di duration obbligazioni per poi passare ad un approfondimento su come si calcola la duration e sul concetto di duration modificata e ancora Macaulay Duration (formula).
Indice
Duration Obbligazioni cosa è
Per definizione la duration è un concetto che racchiude l’analisi su quattro elementi fondamentali presi nel loro insieme: la durata del titolo, la frequenza di emissione delle cedole, gli interessi che vengono offerti in qualità di rendimento e la tipologia di rimborso (può essere con cedola oppure a zero coupon).
Fondamentalmente, quindi, si può dire che la duration delle obbligazioni sia semplicemente la durata media finanziaria e che quindi questo concetto descriva la vita del titolo. Inoltre la duration aiuta a tener conto delle varie prestazioni che vengono attese dal titolo stesso. Si tratta di uno degli indici più importanti da considerare prima di investire in obbligazioni.
Duration obbligazioni: a cosa serve?
Dopo aver dato una definizione di duration, ci sono ora tutti gli elementi per capire a cosa serve questo indicatore.
La duration, semplicemente, permette di valutare il titolo obbligazionario a 360°. Si tratta di una caratteristica molto importante che, soprattutto in alcune situazioni, deve essere presa tassativamente in considerazione. Tra questi casi spicca, per esempio, l’avvicinamento della scadenza, quando la duration diminuisce. Di contro, quest’ultima aumenta quando diminuisce la frequenza delle cedole. Il suo valore è direttamente proporzionale al rischio. Imparando a interpretare in modo adeguato le sue caratteristiche sarà possibile valutare l’effettiva bontà del titolo obbligazionario. Attualmente la duration delle obbligazioni viene considerata come una misura altamente approssimativa del valore di volatilità di un titolo obbligazionario.
Calcolo duration obbligazioni esempio
Come si calcola la duration delle obbligazioni? Generalmente nel calcolo del valore di duration viene compresa una media dei periodi nei quali si eseguono i pagamenti delle cedole oppure dei capitali. Tale durata viene calcolata dal rapporto tra il prezzo di un titolo obbligazionario e i valori attuali. Ovviamente, entrambi i dati a loro volta vengono determinati relativamente al tasso di rendimento.
Eseguendo il calcolo della duration di un titolo obbligazionario si potrà stimare, per esempio, il valore di volatilità di un titolo. In un contesto prettamente tematico, la duration altro non è che la somma delle durate di ogni singolo flusso del titolo relativi al valore degli incazzi che vengono divisi per il prezzo.
Facciamo un esempio per capire meglio come si calcola la duration delle obbligazioni. Mettiamo caso che ci sia una duration con il valore uguale a 3. Se i tassi d’interesse aumentano dello 0,3%, si avrà un prezzo del titolo obbligazionario in calo dello 0,9% (rapporto tra 3 e 0,3%). Nel nostro esempio la variazione è davvero molto piccola, ma in alcuni casi essa può rappresentare un valore anche piuttosto ampio.
Per calcolare la duration viene usata una formula specifica, quella di Frederick Macaulay per la durata media finanziaria. Tale formula è datata 1938, ma è ancor oggi attuale.
Duration modificata: cos’è?
Quello della duration modificata è un concetto che permette di svolgere una completa valutazione della modifica del prezzo quando viene modificato anche il suo rendimento interno. Sotto questo punto di vista la duration modificata può essere considerata come un’aggiunta al calcolo tradizionale della duration obbligazioni.
Calcolo duration modificata
Per calcolare la duration modificata viene usata una semplice formula:
DM = D/(1+r)
In quest’ultima formula, la D è la Duration classica, mentre la R sta per rendimento interno. DM, ovviamente, è a Duration Modificata. Da questa formula si evince il rapporto di derivazione diretta tra duration e duration modificata.
Il calcolo è molto semplice, ma prima di eseguirlo bisogna per forza di cose eseguire anche il calcolo della duration semplice. Solo dopo aver eseguito il calcolo sarà possibile capire se l’investimento nel titolo obbligazionario prescelto fa al proprio caso oppure no.
Macaulay Duration: formula ed esempio
Come già accennato prima, per calcolare la duration viene usata soprattutto la formula di Macaulay:
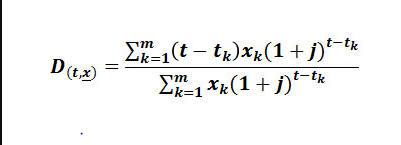
Considerando che si tratta di una formula abbastanza complessa, conviene rivolgere le proprie attenzioni verso Excel. Questo strumento, difatti, dispone di un’apposita funzione chiamata duration, per mezzo della quale è possibile eseguire un calcolo estremamente preciso e accurato. Tutto ciò che serve è indicare alcune informazioni, tra cui:
- la data di acquisto
- la data di scadenza
- l’importo sommario delle cedole (se non ci sono basta mettere 0)
- la frequenza delle cedole
Tutto il resto sarà eseguito dal programma stesso.
L’esempio del calcolo è semplice. Mettiamo X come data e il tasso (i) pari a 0,03. Rendita sarà X diviso per tempo (mettiamo 1000 V1, 1500 V2, 2000 V3 e 2900 V4).
1) Si calcola il valore delle rate al momento con il tasso 0,03 per ogni periodo. La formula è Y (tempo) / (1+0,03). Bisogna fare 4 calcoli, uno per ogni valore di tempo. Il valore di rendita finale è la somma dei valori ottenuti. Facciamo finta questa somma abbia il valore Z
2) Ora si calcolano i singoli pesi seguendo la formula: Peso rendita = V1/Z, V2/Z, V3/Z e V4/Z. Usciranno 4 valori, percentuali.
3) Infine si applica la formula vera e propria: “”Duration rendita = peso 1 x tempo 1 + peso 2 x tempo 2 + peso 3 x tempo 3 + peso 4 x tempo 4″”
Con questi tre passaggi è possibile calcolare la Macaulay Duration e avere così un elemento ulteriore a disposizione per valutare la convenienza dell’investimento.
